How to Pass Deductive Reasoning Tests (Free Practice Tests)

Preparing for deductive reasoning tests is daunting if you have no idea what skills to target and what questions you’ll have.

How to Pass Deductive Reasoning Tests

How to Pass Deductive Reasoning Tests

• a list of key steps to improving your deductive reasoning test results;
• a list of deductive reasoning question types;
• practice examples.

Using a 3-Step Approach for Deductive Reasoning Tests

There are three steps that you can adopt when solving deductive reasoning test questions, including

• Skimming for information;
• Interpreting given inputs into logic collections;
• Processing logic collections into logic maps.

Step 1: Skimming for Information

Skimming is a reading technique that you use to locate information in the given passages within a short amount of time. This skill is essential for better performance on deductive reasoning tests.

The fact that you only have around 2 minutes for each deductive reasoning question and that most deductive reasoning questions involve a great number of relationships make skimming a highly-demanded skill.

Skimming can help you save much of your time in a deductive reasoning test. By skimming, you can get a general idea of what the relationship is about before deciding which part should be focused on for answering the questions.

To practice skimming, you need to get used to moving your eyes rapidly across texts as you will not spend time reading every word. You will pay special intention to subjects, verbs, and sometimes unfamiliar terms just to get an overview of what is happening among given subjects. In general, you can follow the steps below when practicing skimming:

• Read rapidly through the entire paragraph with a focus on subjects and verbs in each sentence;
• Quickly read the questions, and memorize the keywords;
• Think of what you have read in the passage and locate the part of the passage containing keywords of the questions;
• Go back to the passage, and read the entire sentence for the answer.

You should learn how to resist temptation or get rid of the habit of stopping to read everything in detail. When you skim, you may face the risk of missing something, however, skimming doesn’t mean understanding everything in one take but instead having an overview for later focused reading.

Read more

What is Deductive Reasoning?
Are Deductive Reasoning Tests Hard?

Step 2: Interpreting Given Inputs Into Logic Collections

Since deductive reasoning tests are all about testing your ability to make a deduction, you need to practice how to interpret information into logic collections. This is the next step and also the next skill on the preparation list when solving a deductive reasoning question.

Once finishing skimming, you’ll have a list of subjects that are in the given passage. Your job is to group them into different logic collections. Collections in this case mean the interrelationship of each subject towards another. For example, the passage describes the interrelationship among A, B, and C. You will have to figure out the interrelationship between A and B, B and C, and C and A if any.

Step 3: Processing Logic Collections Into Logic Maps

The final step is to map out the relationship among all mentioned subjects using the logic collections you have figured out. For complicated deductive reasoning questions where you have a great number of subjects, you will need this skill to have a structured overview of relationships among subjects without confusing yourself.

Both this step and the previous one require a thorough understanding of deductive reasoning rules, logic, and artificial languages that help indicate the interrelationship of given subjects.

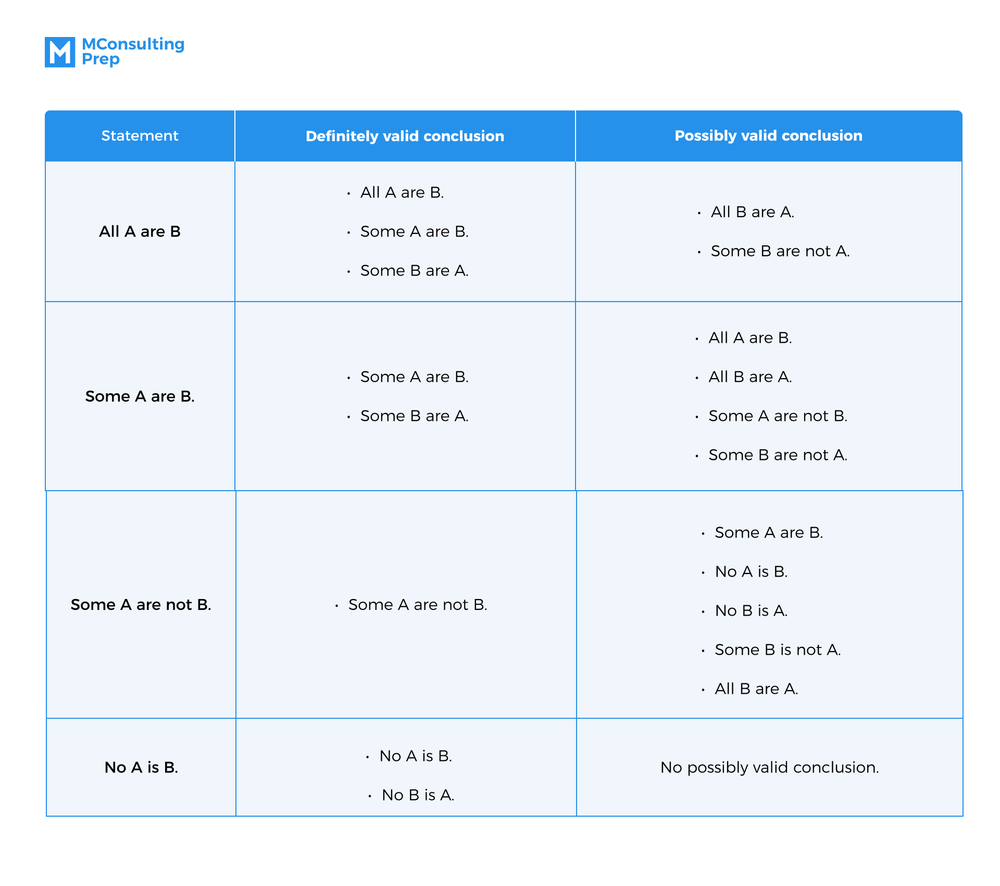
Adopt 7 Quick Rules for Syllogism Conclusion Validity

You can memorize the 7 below syllogism formulas to quickly test the validity of any syllogism questions you might be having in your deductive reasoning tests.

• All+All premises equal an All conclusion.
• All+No premises equal a No conclusion.
• All+Some premises equal a No conclusion.
• Some+All premises equal a Some conclusion.
• Some+No premises equal a Some Not conclusion.
• Some+Some premises equal a No conclusion.

There are also 4 rules for conclusion possibilities of syllogism questions:

• If All A is B -> Some B is Not A is a possible conclusion.
• If Some B is Not A -> All A are B is a possible conclusion.
• If Some A is B -> All A is B is a Possibility & All B are A are possible conclusion.
• The conclusion is only correct if it justifies all possible conclusions.

Use Euler and Venn Diagram for Categorical Syllogism

For categorical syllogism questions, using the Venn and Euler diagrams is a helpful method to quickly make a valid conclusion.

Euler vs. Venn Diagram

Euler diagrams present

• real-world combinations of all subjects;
• and real-world intersections of all subjects;

while Venn diagrams give you all possible combinations and intersections.

In a deductive reasoning question, an Euler diagram helps you work with only information stated in the premises. Meanwhile, a Venn diagram helps you map out all possibly valid conclusions that are not directly stated in the premises.

In a Venn diagram, all circles must mutually overlap. This is not a requirement with Euler diagrams.

It’s highly recommended that you prioritize using Euler diagrams over Venn diagrams for your deductive reasoning questions. The reason behind this is that an Euler diagram helps you focus on only what is presented in the questions; whereas Venn diagrams may distract you with the presentation of all possibilities.

You should only use Venn diagrams when you can’t test the validity of all the given conclusions. That’s when Venn diagrams give your more conclusion possibilities for the given premises.

Euler and Venn Diagram in Solving Syllogism Questions

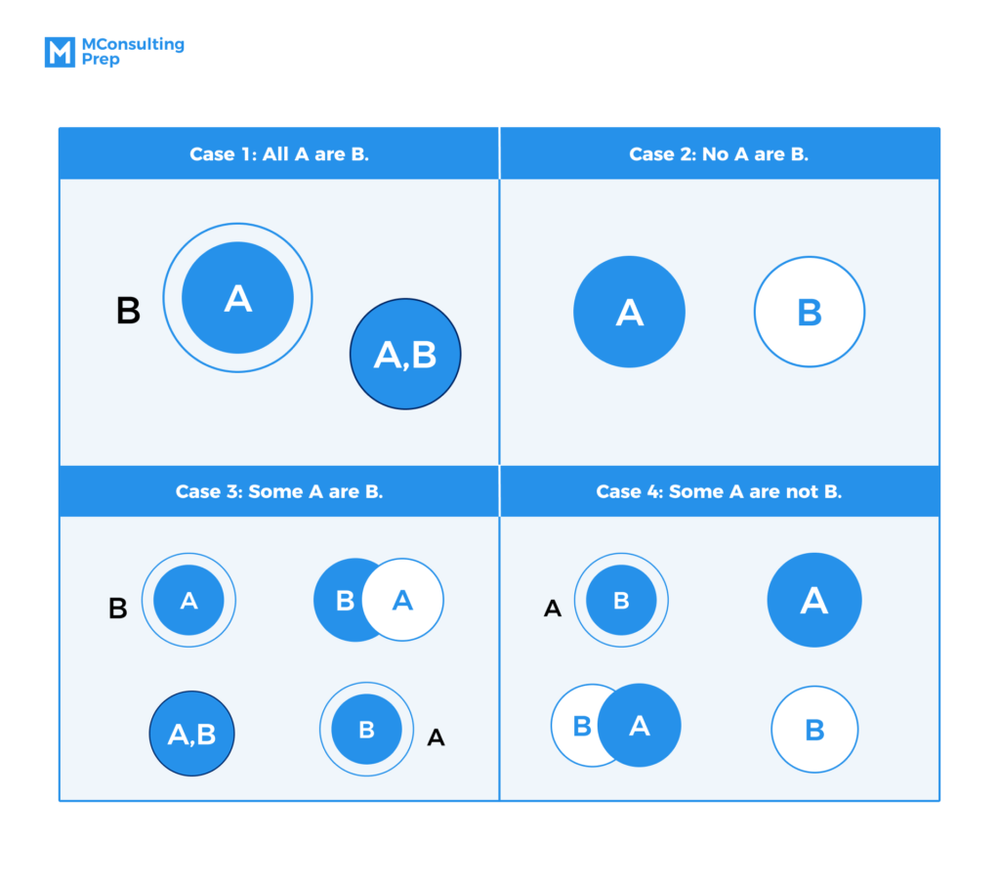
Here’s a sum up of diagram presentations for common premises:

• All A are B: The diagram represents this case will be either a circle lying within another circle or two circles overlapping each other.
• No A is B: The diagram represents this case will be two separate circles with no intersection.
• Some A are B: There are four possible diagrams that can represent this statement: one circle lies within another one interchangeably; two circles overlap each other; or two circles intersect each other.
• Some A are not B: There are four possible diagrams that can represent this statement: one circle lies within another one; two circles intersect each other; two separate circles with no intersection interchangeably for two subjects.

We also include some examples where we use Euler diagrams to work out deductive reasoning questions.

Syllogism questions

Syllogisms are the most popular question types of deductive reasoning. In a syllogism, there are two premises and one conclusion. The first premise is known as the “major premise;” and the second premise is known as the “minor premise.” Both the premises share a subject called the middle term. Let’s take the syllogism below as an example:

All mammals are animals.
Dolphins are mammals.
Therefore, dolphins are animals.

In the syllogism above, the major premise is “All mammals are animals.”; the minor premise is “Dolphins are mammals.” and the middle term is “mammals“.

The conclusion in a syllogism always follows the truth stated in two premises.

Logical reasoning of syllogism questions involves an abstract thinking process: You solve the question by organizing/mapping/connecting a series of premises into a particular order that can justify the conclusion.

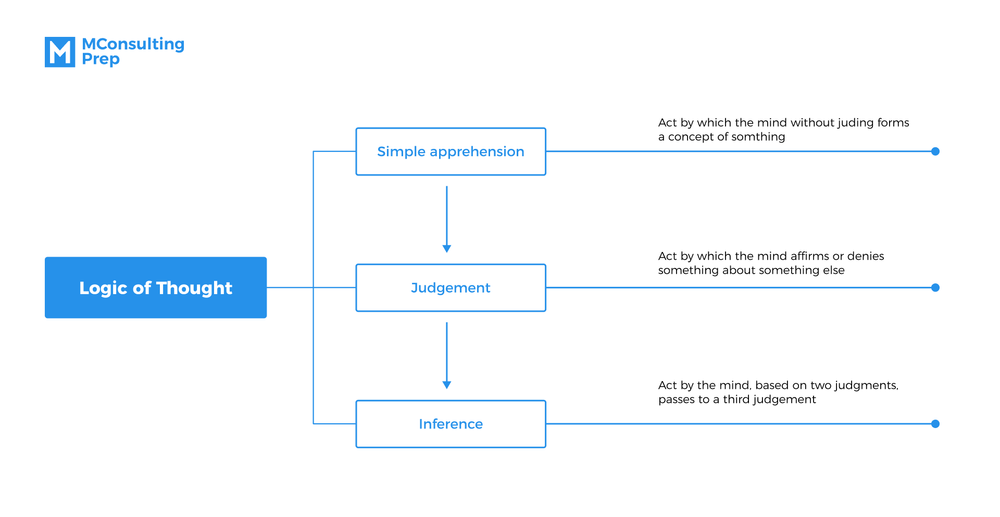
In other words, you go through a making-inference process – a thought process of creating new judgment based on the available information (i.e premises).

There are some key terms to memorize when it comes to a syllogism.

Syllogistic Fallacy: a syllogistic fallacy is a mistake in a deductive logic argument, where the conclusion does not follow the premises.

Example:

No philosophers are giraffes.
All giraffes are mammals.
Therefore no philosophers are mammals.

Though it is true that there are no philosophers that are giraffes, and that all giraffes are in fact mammals. These do not negate the fact that philosophers (humans) are giraffes. The alternative name for this fallacy is the fallacy of the undistributed middle.

The above syllogism will be valid if written this way:

No philosophers are giraffes.
All mammals are giraffes.
Therefore no philosophers are mammals.

Enthymemes: The term refers to deductive arguments that function similarly to a syllogism, but there is at least one implicitly true premise. In other words, it is assumed that the audience knows that premise is true.

Example

All mammals, except platypus and the echidna, give birth.
Therefore, chimpanzees give birth.

The implicit premise here is “Chimpanzees are mammals”, and it’s assumed to be acknowledged by everyone.

Valid: A syllogism is valid when the conclusion follows the truth of the premises. The conclusion can’t be false when the premises are true.

Sound: A syllogism is sound when the deductive argument is valid and both the premises are true statements. A syllogism can be valid without being sound.

Example

All birds can fly.
Ostriches are birds.
Therefore, ostriches can fly.

This is a valid argument since the conclusion follows the premises, yet not a sound argument due to having one of the premises that is not a true statement.

Reductio ad impossibile: this is a method to check the validity of an argument. If it is contradictory to deny the conclusion while accepting the premises, then the argument is valid.

These key terms also represent 5 syllogism rules that ensure the validity of all syllogism arguments.

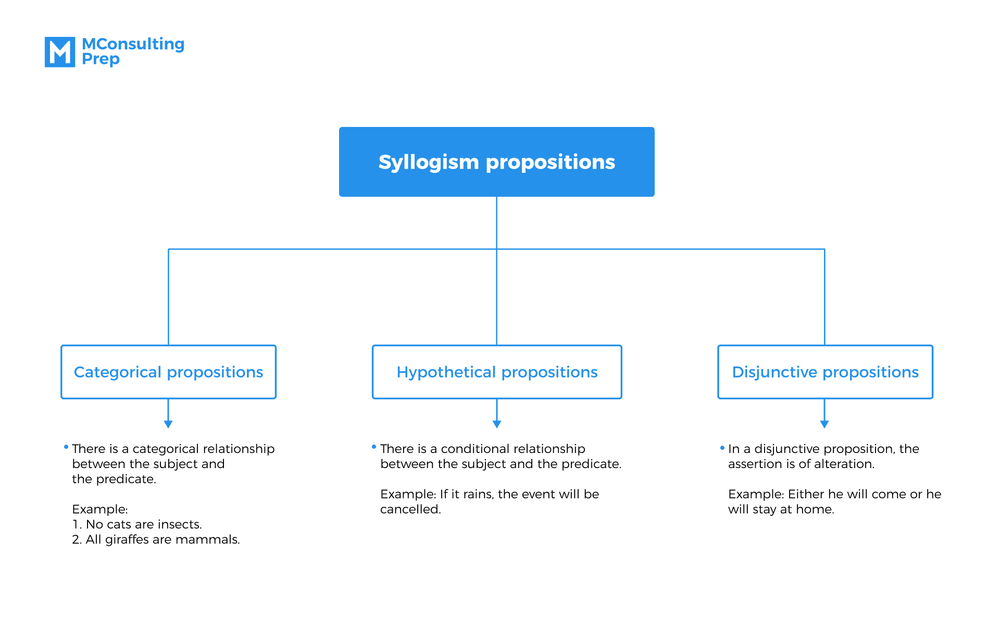
There are three main types of syllogism that you’re more likely to encounter in a deductive reasoning test:

• Categorical (Premises are categorical propositions)
• Hypothetical (Premises are hypothetical propositions)
• Disjunctive (Premises are disjunctive propositions)

Categorical Syllogism

A categorical syllogism is a syllogism featuring three classes in its premises and conclusion; each of these classes appears in exactly two propositions.

In simpler words, a categorical syllogism demonstrates the qualities of a specific category and then makes a statement on an item that contains those qualities.

Let’s take an example for better understanding.

Example

Some philosophers are leaders.
All leaders are think tanks.
Therefore, some philosophers are think tanks.

This example is a categorial syllogism since it has three propositions with three classes (philosophers, leaders, think-tanks), each of which appears two times separately in the propositions.

You can easily recognize such a categorical syllogism in your deductive reasoning test. These syllogisms are always written in the standard form, as a rule of thumb. It means the major term (philosophers) must appear in the major premise, the middle term must be in both the major and minor premise (leaders), and the minor term must be in the minor premise.

Hypothetical Syllogism

A hypothetical syllogism (also known as conditional syllogism) has a hypothetical statement in the form of “if … then”. The syllogism is not entirely hypothetical, but rather has one of its premises being hypothetical.

This type of syllogism is often structured with a conditional major premise, and an unconditional minor premise together leading to an unconditional conclusion:

• A conditional major premise;
• An unconditional minor premise;
• An unconditional conclusion.

A hypothetical syllogism has two main parts: the antecedent and the consequent.

The antecedent is the “IF” part of the premise stating the condition under which the “THEN” part is true.

The consequent is the “THEN” part which is the consequent of what follows the “IF” part, or in case the “IF” part is true.

The conclusion of a hypothetical syllogism is valid when the premise affirms the “IF” part (modus ponens), or denies the “THEN” part (modus tollens).

• Modus ponens: This is one of the main ways to test the validity of the conclusion, which is to affirm the antecedent. In other words, the minor or the second premise will indicate the antecedent and that the “if” clause is true. In that case, the “then” part will be true as a result. 

Example

If today is Sunday, then Lisa will have a day off.
Today is Sunday.
Therefore, Lisa will have a day off.

• Modus tollens: Another way to test the validity of the conclusion is to deny the consequent. In other words, if the minor or the second premise denies the truth of the “THEN” clause, the “IF” clause must not be a reality, or the “IF” clause can’t happen. Modus tollens is the reverse version of modus ponens.

Example

If today is Sunday, then Lisa will have a day off.
Today is not Sunday.
Therefore, Lisa will not have a day off.

Disjunctive Syllogism

A disjunctive syllogism is a form of a deductive argument. It has one premise presenting two possibilities, and one premise determining which possibility happens. Disjunctive syllogism in propositional logic is a valid rule of inference.

A disjunctive syllogism will look like this:

Either P or Q is true.
P is false.
Therefore Q is true.

Example

Either mom or dad will come to the monthly parent meeting.
Mom came to the monthly parent meeting.
Therefore, dad didn’t come to the monthly parent meeting.

Let’s Practice Some Deductive Reasoning Examples

Example 1

Statements:

All tables are phones
Some phones are gadgets

Conclusion: Some gadgets are not tables.

A. CONCLUSION FOLLOWS
B. CONCLUSION NOT FOLLOW

Correct answer: B

Explanation:

Denote:

~ Ta: Tables
~ Ph: Phones
~ Ga: Gadgets

1. Analyzing the statements:

All tables are phones ⇒ Ta ⊂ Ph

Some phones are gadgets ⇒ Ph ∩ Ga

Using the Euler circle, we have the following diagram:

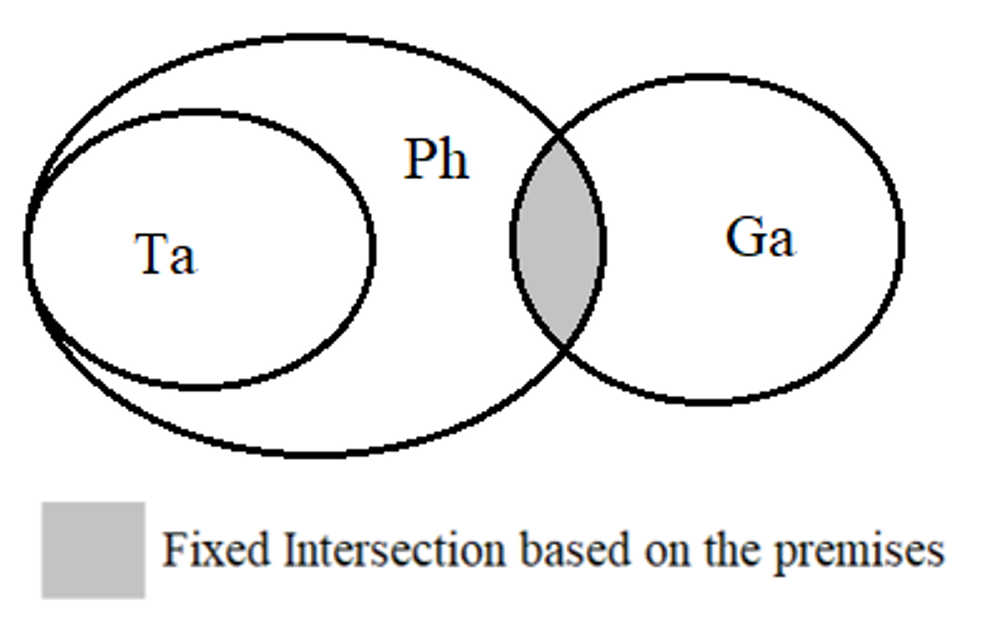
2. Checking the conclusion: Some gadgets are not tables.

If one is Tables, then it must be Phones (Ta ⊂ Ph)

If one is Phones, then it can be Gadgets (Ph ∩ Ga)

⇒ If one is Gadgets, it can be Tables.

⇒ Some Gadgets can be Tables.

⇒ Data is insufficient to deduce that: Some gadgets are not tables.

Therefore, CONCLUSION NOT FOLLOW.

Example 2

Statements: 

Some mountains are rivers
Some rivers are deserts
All deserts are roads

Conclusion: Some roads are rivers.

A. TRUE
B. FALSE
C. INSUFFICIENT INFORMATION

Correct answer: A

Explanation:

Denote:

~ Mo: Mountains
~ Ri: Rivers
~ De: Deserts
~ Ro: Roads

1. Analyzing the statements:

Some mountains are rivers ⇒ Mo ∩ Ri

Some rivers are deserts ⇒ Ri ∩ De

All deserts are roads ⇒ De ⊂ Ro

Using the Euler circle, we have the following diagram:

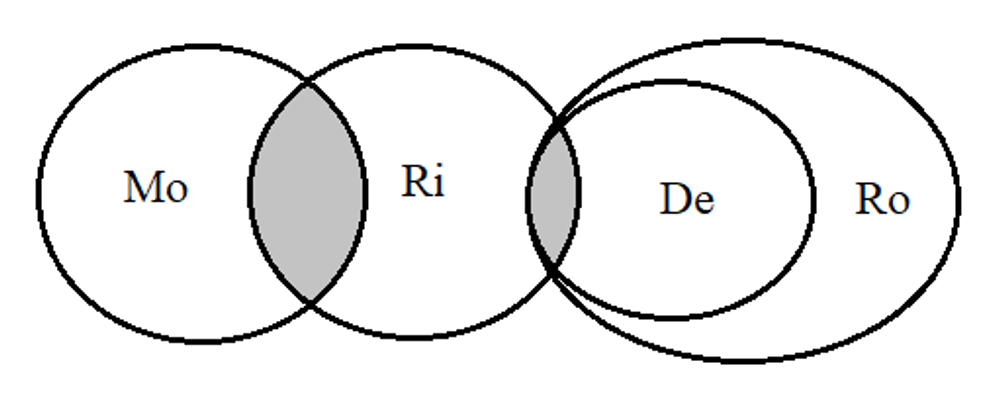
2. Checking the conclusion: Some roads are rivers

If one is Rivers, then it can be Deserts (Ri ∩ De)

If one is Deserts, then it must be Roads (De ⊂ Ro)

⇒ If one is Rivers, it can be Roads.

⇒ Some roads are rivers.

Therefore, the conclusion is TRUE.

Example 3

Statements:

All coats are shirts
Some shirts are caps
No caps are trousers

Conclusions:

1. Some coats are caps.
2. Some trousers are not shirts.

Which conclusion definitely follows the statements above?

A. Only conclusion I follows
B. Only conclusion II follows
Both conclusions I and II follow
None of the above

Correct answer: D

Explanation:

Denote:

~ Co: Coats
~ Sh: Shirts
~ Ca: Caps
~ Tr: Trousers

1. Analyzing the statements:

All coats are shirts ⇒ Co ⊂ Sh

Some shirts are caps ⇒ Sh ∩ Ca

No caps are trousers ⇒ Ca ≠ Tr

Using the Euler circle, we have the following diagram:

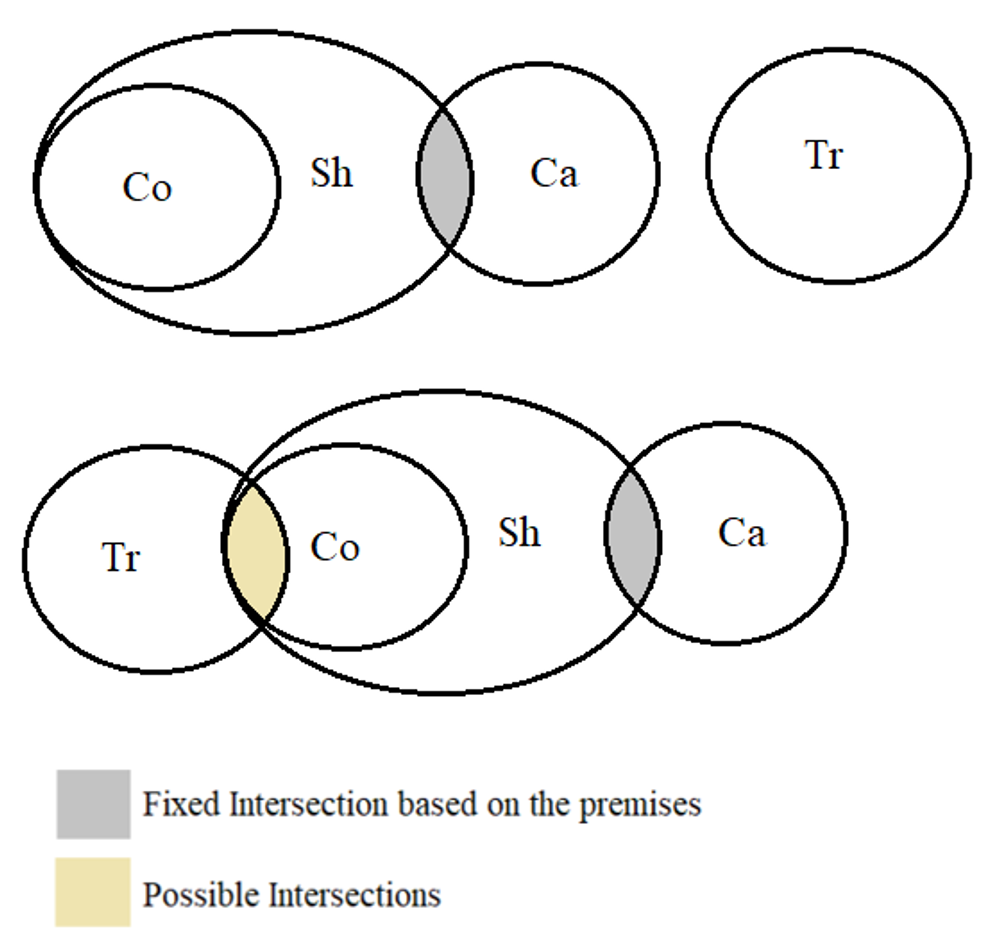
2. Checking the conclusion:

Some coats are caps: From the given premises, some coats can be caps, so this is a possibility since data is insufficient to support the conclusion.

⇒ Conclusion I does not follow.

Some trousers are not shirts: From the given premises, some trousers can be shirts or cannot be, so this is a possibility since data is insufficient to support the conclusion.

⇒ Conclusion II does not follow.

Therefore, none of the conclusions definitely follow the statements.

Example 4

Statements:

Some berries are red.
Some grapes are green.
All grapes are berries.

Which conclusion is true based on the given statement?

A. Some grapes are red.
B. Some berries are green.
C. No berry is green.
D. All berries are red.

Correct answer: B

Explanation:

Denote:

~Br: Berries
~Grp: Grapes
~R: Red
~Grn: Green

1. Analyzing the statements:

Some berries are red. ⇒ Br ∩ R

Some grapes are green. ⇒ Grp ∩ Grn

All grapes are berries. ⇒ Grp ⊂ Br

Based on the above analysis, we can draw the Euler Diagram

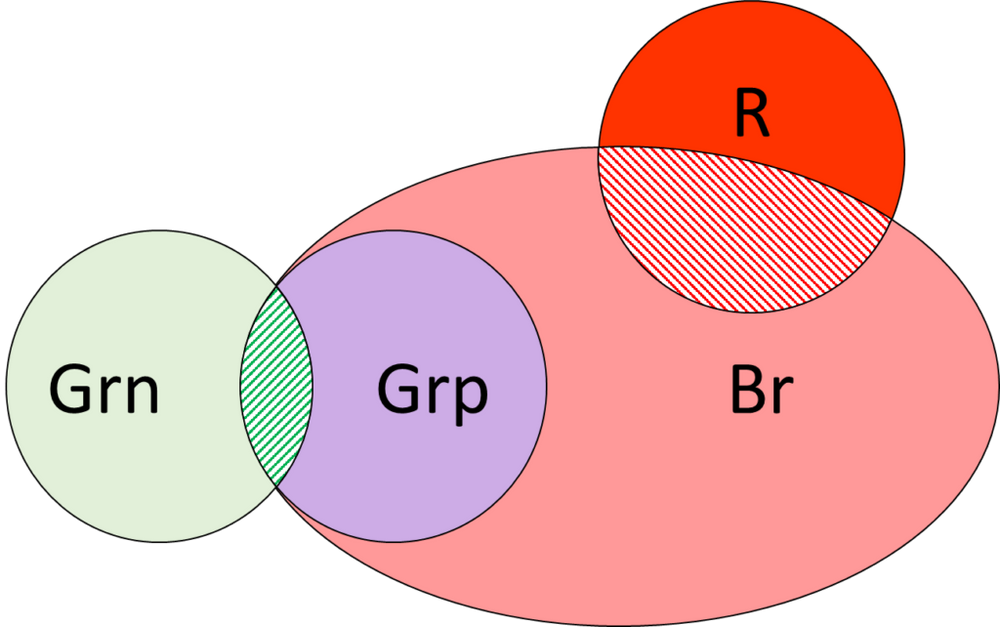
2. Checking the conclusion:

Some grapes are red. ⇒ Grp ∩ R

Based on the diagram, we can see that Grape and Red can either intersect with each other or not; therefore, we do not have enough information to reach this conclusion ⇒ Eliminate/

Some berries are green. ⇒ Br ∩ Grn

Based on the diagram, we can see that: a Grape is always a Berry; therefore, there are always some green grapes which are also berries ⇒ Conclusion is definitely true.

No berry is green. ⇒ Br ∩ Grn

Similarly, we can see that there are always some green grapes which are also berries ⇒ “No berry is green” can never happen ⇒ Conclusion is definitely false ⇒ Eliminate.

All berries are red. ⇒ Br ⊂ R

Based on the diagram, we can see that Berry and Red can either partly intersect with each other or include each other; therefore, we do not have enough information to reach this conclusion ⇒ Eliminate.

Example 5

Statements:

Each van is a car.
Some vans run with electricity.
Many cars drive fast.

Which conclusion is true based on the given statement?

A. No van drives fast
B. Only fast-driving cars run with electricity
C. At least one car runs with electricity
D. All vans are cars running with electricity

Correct answer: C

Explanation:

Denote:

~Car
~Van
~Drive fast
~Run with electricity

1. Analyzing the statements:

Each van is a car. ⇒ Van ⊂ Car

Some vans run with electricity. ⇒ Vans ∩ Run with electricity

Many cars drive fast. ⇒ Car ∩ Drive fast

Based on the above analysis, we can draw the Euler Diagram

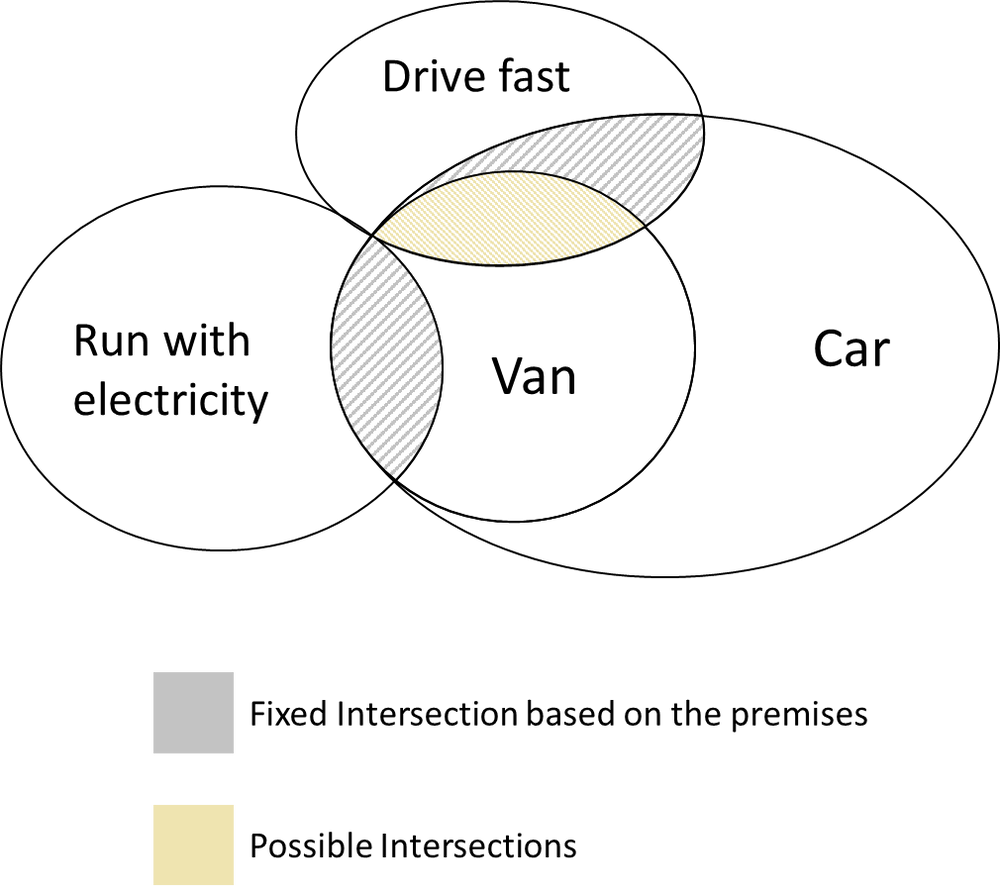
2. Checking the conclusion

No van drives fast ⇒ Van ≠ Drive fast

Based on the Euler Diagram, we can see that, there is a possibility that Drive fast and Van can intersect as long as Drive fast intersects with Car

⇒ We do not have enough information to reach the conclusion “No Van drives fast” ⇒ Eliminated.

Only fast-driving cars run with electricity ⇒ All cars that run with electricity drives fast ⇒ (Car ∩ Run with electricity) ⊂ Drive fast

Based on the Euler Diagram, we can see that, there is a possibility that Drive fast and Run with electricity – as long as Run with Electricity intersect with Van and Drive fast intersect with Car.

⇒ We do not have enough information to reach the conclusion “Only fast-driving cars run with electricity ” ⇒ Eliminated.

At least one car runs with electricity ⇒ Some car runs with electricity ⇒ Car ∩ Run with Electricty.

Based on the Euler Diagram, we can see that: Car always includes Van and Van intersects with Run with Electricty ⇒ Cars which are Van, runs with Electricity

⇒ The conclusion is true.

All vans are cars running with electricity

Based on the Diagram, there is still a posibility that not all vans run with electricity ⇒ ⇒ We do not have enough information to reach the conclusion ⇒ Eliminated.

You can assess our deductive reasoning test package to see more 200 examples with a detailed answer guide. To make your experience better, we offer the free trial to help you have a look at the product before purchasing!