Are Deductive Reasoning Tests Hard?

There are several different factors that contribute to the difficulty level of deductive reasoning tests. In this article, you’ll learn how hard a deductive reasoning test can be.

Are deductive reasoning tests hard?

There are two main factors deciding the difficulty level of a deductive reasoning test: the number of details and time constraints. In a deductive reasoning test, the increasing number of details makes it difficult for you to navigate the relationship among inputs, and time constraints add up as a factor hindering your performance.

More context and input means increasing difficulty

As deductive reasoning tests are given in long-worded forms, more context and input added to such word contexts means increasing difficulty. The more details and connections a deductive reasoning question have, the more distracted you become when identifying necessary information for the answer.

Strict time allowance adds up to difficulty levels

On average you will have around 66 seconds to handle a deductive reasoning question, which means a lot of struggle without pre-test practice. Within these 66 seconds, you often have to process a great deal of information before deciding what is needed for the answer and using deductive reasoning to form a conclusion for the answer.

There’s no better way to get yourself familiar with withstanding the time constraint than regular practice with proper strategy. Once you know how to cope with the pressure of time, you’ll do your deductive reasoning test in a much calmer manner.

What to prepare for deductive reasoning tests?

To take a deductive reasoning test with confidence, you’ll need to brush up on the following skills:

• Skimming for information;
• Interpreting given inputs into logic collections;
• Processing logic collections into logic maps.

Below is an example of how we use these skills in solving a complex deductive reasoning question.

Example:

Jack, Thomas, and Peter are three remarkable men, each having some remarkable characteristics.

1. Just two are remarkably intelligent, just two are remarkably good-looking, just two are remarkably talented, and just two are remarkably rich.

2. Each has no more than three remarkable characteristics.

3. Of Jack it is true that: if he is remarkably intelligent, he is remarkably rich.

4. Of Thomas and Peter it is true that: if he is remarkably good-looking, he is remarkably talented.

5. Of Jack and Peter it is true that: if he is remarkably rich, he is remarkably talented.

Who is not remarkably rich?

As you can see, this is a complicated question with several inputs. You need to skim for necessary inputs and keywords since you won’t have enough time for a careful and thorough read. For the question above, you have to skim for all related information to work out the relationship of the characteristics among Jack, Thomas, and Peter.

From the gathered information, you can start interpreting such information into collections of logical arguments as follows.

For Jack:

• From [3] and [5] if he is intelligent, he is talented. From [5] if he is rich, he is talented. From [1] and [2], if he is neither rich nor intelligent, he is talented.

For Peter:

• From [4] if he is good-looking, he is talented. From [5] if he is rich, he is talented. From [1] and [2], if he is neither rich nor beautiful, he is talented.

For Thomas:

• From [1] Thomas is not talented. Then from [4], Thomas is not good-looking. So from [1] and [2], Thomas is intelligent and rich.

After having such logic collections, we continue to map the relationship of these arguments for a more well-rounded picture of deductive reasoning arguments.

We can tell from these logic collections that:

• In any case, Jack is talented;
• In any case, Peter is talented;
• From [1] and the fact that Thomas is not good-looking, Jack and Peter are both good-looking;
• From [2], and [3], Jack is not intelligent;
• From [1], and the fact that Jack is not intelligent, Peter is intelligent;
• From [1] and [2], and the fact that Peter is intelligent, Jack is rich and Peter is not rich.

If you want to practice deductive reasoning tests more, try MConsultingPrep's offer! Our deductive reasoning test package provides 200+ categorized questions with a step-by-step answer guide.

Common mistakes to avoid

When taking a deductive reasoning test, there are a few common mistakes that you have to avoid for better test results which include:

• Using common sense in deciding the logical arguments;
• Misunderstanding quantifiers;
• Creating false dilemmas (or Fallacies).

Using common sense

You need to avoid using common sense while doing deductive reasoning tests, since common sense and prior knowledge may affect the validity of your deductive reasoning argument. Your job is not to determine whether the premises are true based on your previous knowledge/common sense, and a deductive argument doesn’t necessarily need to be sound to be logical.

The main difference between common sense and deductive reasoning is that common sense is learned while deductive reasoning is based solely on analytical data which you draw corresponding conclusions from. This is the key point to help you differentiate between common sense and deductive reasoning, and avoid using common sense in your deductive reasoning questions.

Here’s an example for you.

All the philosophers are males. Socrates was a philosopher.

Conclusion:

1. Socrates was male.

2. Females cannot be philosophers.

If you use your common sense in this syllogism, you will assume that the second conclusion is not true. However, based on the details given in the premises, the second conclusion is still a valid deductive argument.

Misunderstanding quantifiers

In deductive reasoning tests, especially tests including syllogism questions, you may find yourself struggling to determine relationships among inputs due to the misunderstanding of quantifiers.

A syllogism usually consists of three quantified sentences (two premises and one conclusion) and three variables. Among different types of syllogisms, categorical syllogisms are where you have to deal with quantifiers on a regular basis. Its inferences are often based on quantifiers such as EVERY, MOST, SOME, AT MOST, AT LEAST, NO, NOT ALL, etc. and therefore misinterpreting one of these quantifiers results in you implying the wrong connection among variables.

Every categorical syllogism is preceded by a quantifier based on two aspects: membership and coverage. For membership, the terms are “Affirmation” and “Negation”; for coverage, the terms are “Universal” and “Particular”. Syllogisms use popular quantifiers to indicate such terms as follows:

• Affirmative universal: ALL;
• Affirmative particular: SOME;
• Negative universal: NO;
• Negative particular: SOME …NOT, NOT ALL, etc;

These four commonly seen quantifiers are not as simple as you think, and sometimes they are more inclusive than they may appear. For example, the term SOME means “at least one and possibly all”.

We have another example for you using the VENN diagram to demonstrate all the possible interpretations of the quantifier SOME in a syllogism.

Example:

Premise 1: Some men are engineers.

Premise 2: Some engineers are rich.

Conclusion: Some men engineers are rich.

Premise 1: Some men (a) are engineers (b).

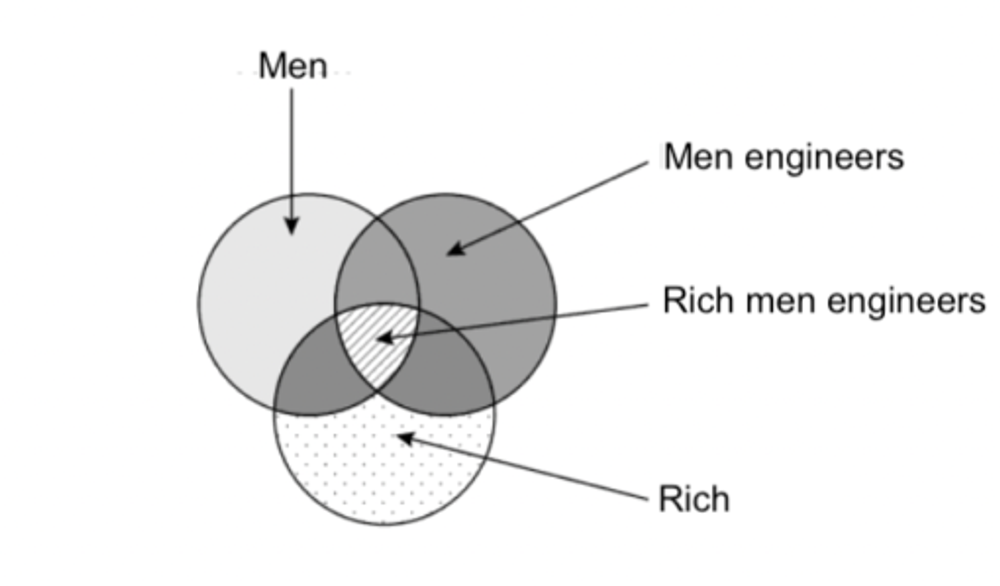
We have a VENN diagram illustrating the interpretation of the above syllogism as follows:

Creating false dilemmas (Fallacies)

Deductive fallacies are also among the mistakes you need to be aware of. In deductive reasoning tests or any tests that examine deductive reasoning skills, you may encounter multiple-choice questions in which you have to choose one correct answer. In that case, you’re likely to choose answers involving deductive fallacies.

There are four common types of deductive fallacies which include:

• Affirming the disjunct
• Affirming the consequent
• Denying the antecedent
• Invalid syllogisms (syllogistic fallacies)

By affirming a disjunct in a deductive reasoning question, it means when given an either/or situation, you wrongly assume that if one statement is true, the other one cannot be true. An example of affirming a disjunct would be: I am at home or I am in town. I am at home. Therefore, I am not in town.

Affirming the consequent which is also called a fallacy of the converse, is when you take a true statement and wrongly assume the validity of its converse. An example of this would be: If it’s a wolf, then it growls. It growls. Therefore, it’s a wolf.

Denying the antecedent happens when the minor premise of a propositional syllogism denies the antecedent of a conditional statement. The fallacy lies in assuming that the consequent must also be denied if the antecedent is denied. The consequent conclusion, therefore, is invalid because the truth of the premises does not guarantee the truth of the conclusion. Here’s an example: I just sent you a message. If you responded, that means you’ve received it. You didn’t respond, so that means you haven’t received it.

You’ll also need to make sure that your deductive reasoning in syllogism questions always follows 5 RULES that ensure the syllogisms’ validity:

• The middle term must be distributed at least once. The fallacy lies in the undistributed middle term;
• If a term is included in the conclusion, it must also be in its corresponding premise. The fallacy lies in either the undistributed minor term in the subject or the undistributed major term in the predicate;
• A syllogism cannot have two negative premises. The fallacy lies in the exclusive premises;
• A negative premise must have a negative conclusion and vice versa. The fallacy lies in either stating an affirmative conclusion based on a negative premise or stating a negative conclusion based on an affirmative premise;
• Two universal premises must have a universal conclusion. The fallacy lies in the particularity of the conclusion.