How to Pass Numerical Reasoning Tests? (2024 Essential Tips)

Tips to pass the numerical reasoning test

To pass a numerical reasoning test, it’s important to know what to practice and how to practice. Here are the most crucial things to master before taking your upcoming numerical reasoning test:

• Processing math in different contexts: daily, business, and finance
• Filtering data in the form of tables, bars, lines, pie charts, caselet  
• Making quick and accurate calculations

Learning to process math in different contexts

You will likely encounter a great deal of math calculation in different contexts in your numerical reasoning tests.

There are different graphs, tables, and word problems portraying different daily, business, or finance-related scenarios that you need to work on for the questions after that.

There might be between two and five questions for each set of presented data, with four or five answers for each question. Your task is to decide which correct answer is derived solely from the numerical data presentation.

Therefore learning to process math in different contexts is necessary if you want to pass your numerical reasoning test. Generally, there are three main math contexts that you might come across which are daily, business, and finance.

In daily contexts, you are expected to know several math formulas such as: 

Practicing filtering data in different forms

Filtering data in different forms is what helps you handle data interpretation questions (long context) where there is often a great deal of distracting data.

Calculations needed for the final answer are not what makes data interpretation complex, but rather the abundant details provided in the questions.

As data interpretation questions are usually given in different data forms such as tables, bars, lines, pie charts, and caselet, you can practice filtering data by trying to resolve questions involving data presentation of such forms.

For a better understanding of how you might attempt to solve these questions, we have a couple of examples for you.

Table chart question example:

A factory’s production team has three workers (worker 1, worker 2, and worker 3) to manufacture three products X, Y, and Z. Each worker takes a daily shift of 12 hours. The following table gives the time taken (in minutes) by each worker to manufacture 1 unit of each of the products.

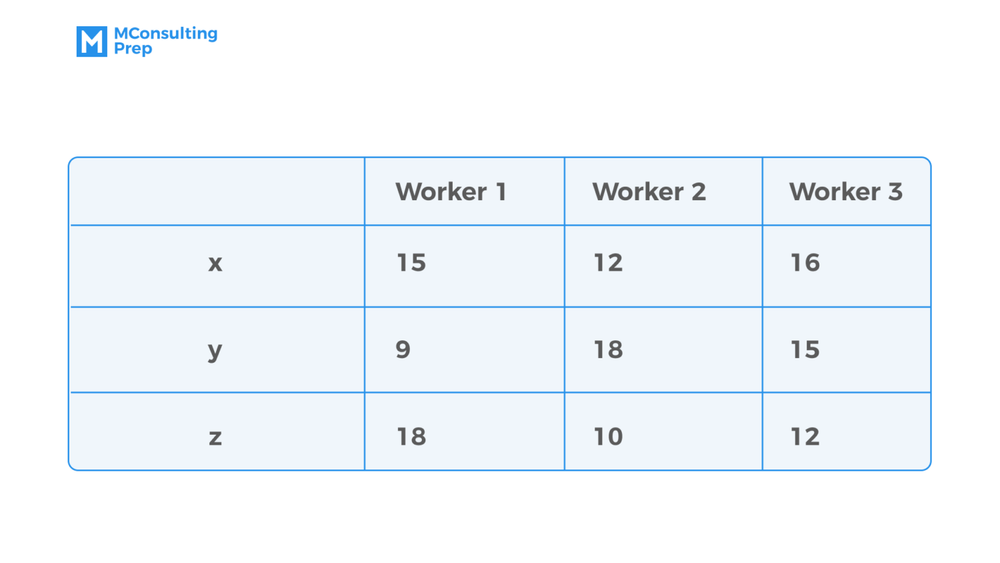
Q: What is the maximum number of products that can be manufactured in a day?

Since the question asks for the maximum quantity of products that can be manufactured in a day, we need to look for the minimum production time of each product.

From the table’s data, we can see that the minimum production time for each product X, Y, and Z is 12, 9, and 10 minutes respectively.

Each worker works for 12 hours or 720 minutes so the total production time of each product is 720 minutes. Within 720 minutes, there’ll be 72 units of Z, 80 units of Y, and 60 units of X that can be manufactured by three workers, respectively. Thus, the maximum number of units that can be manufactured in a day is 212.

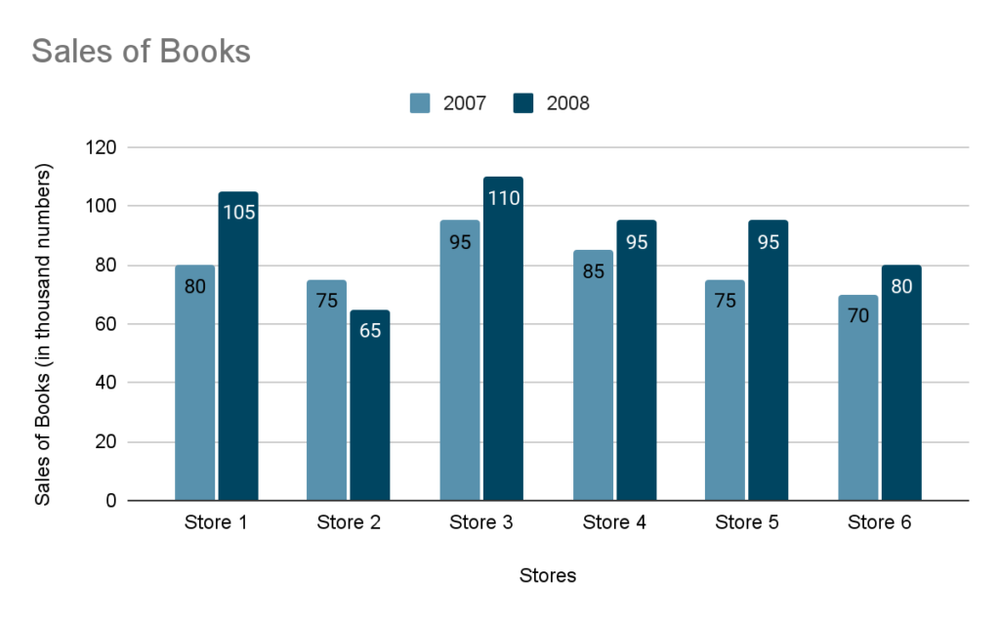
Bar chart question example:

The bar graph given below shows the sales of books (in thousand numbers) from six different stores of a publishing company during two consecutive years 2000 and 2001.

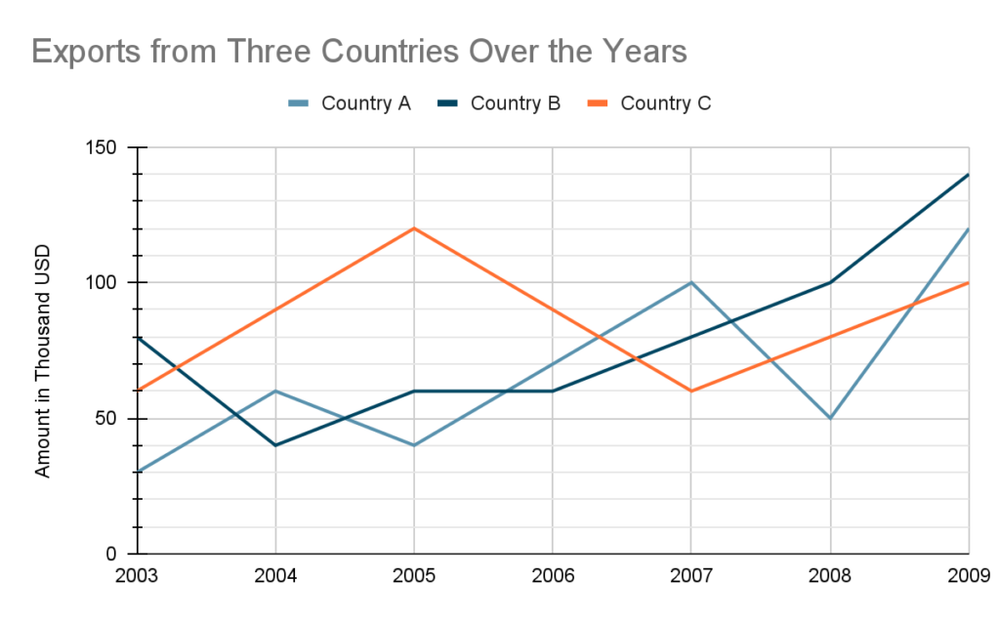
Line chart question example:

Study the following line graph and answer the questions.

Pie chart question example:

The following pie chart demonstrates the percentage distribution of the expenditure in a book publishing process. Study the pie chart and answer the questions based on it.

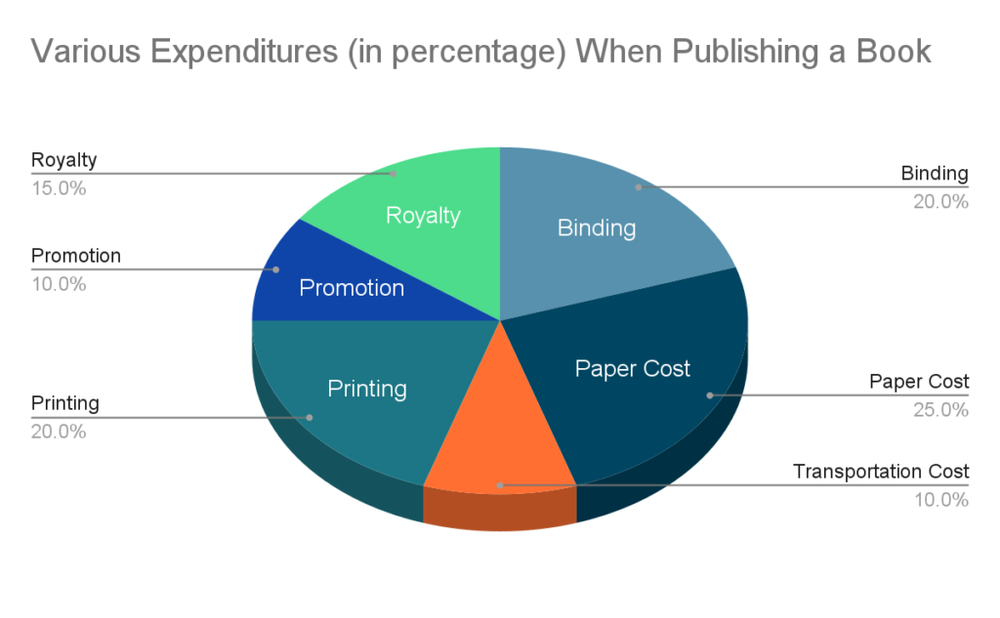
Q: To release 1000 books, the publisher has to pay 5600 USD as printing cost, what will be the amount of royalty to be paid for these books?

First, we see that printing costs account for 20% of the total expenditures, therefore we can easily figure out the total expenditure amount which is 5600 20% = 28000 USD.

Since the royalty amount accounts for 15% of the total expenditure amount, we then know the royalty amount for releasing 1000 books will be 28000 15% = 4200 USD.

Caselet question example:

Three colleagues Jack, Rachel, and Simon spend 12%, 14%, and 16% of their monthly salary on traveling respectively, and half of the remaining amount on savings. Jack and Simon have the same amount of monthly salary, and the monthly saving of Jack is 360 USD more than that of Simon. The total expenditures of Jack and Rachel together on traveling is 1240 USD more than that of Simon.

Q: What is the monthly expenditure of Jack and Rachel together on traveling?

The monthly salary of Jack and Simon are the same and Jack’s monthly saving is 360 USD more than that of Simon

44X – 42X = 2X = 360

X = 180

The total expenditures of Jack and Rachel together on traveling is 1240 USD more than that of Simon.

12X + 14Y = 16X + 1240

14Y = 4X + 1240 = 720 + 1240 = 1960

Y = 140

The monthly expenditure of Jack and Rachel together on traveling = 12X + 14Y = 12 × 180 + 14 × 140 = 2160 + 1960 = 4120 USD.

Excelling at making quick and accurate calculations

What decides whether or not you will pass the test is your skill at making quick and accurate calculations. This skill helps you speed up doing simple calculations, which also helps you save time to work out more complicated questions.

The key to becoming excellent at performing quick and correct calculations is through daily practice of mental math, and basic to complex calculations such as calculations with big numbers, decimals, and serial calculations. 

Below are a few examples for you to try.

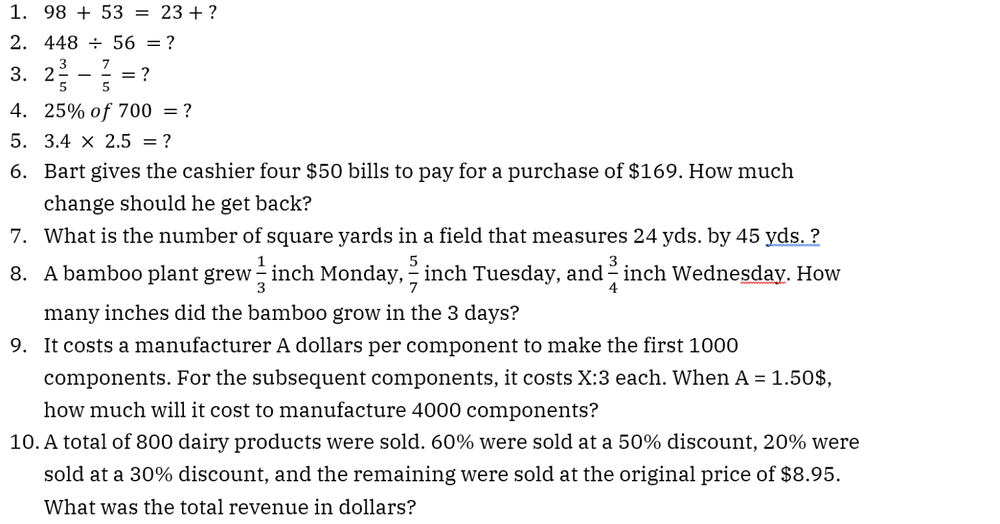
What to expect in numerical reasoning tests?

Numerical reasoning tests often include calculation, estimation, numerical sequence, and data interpretation questions.

Data interpretation questions are more likely in tests for higher-level positions such as those in management. In contrast, other question types are more popular in tests at the administrative and executive levels.

For basic calculation and estimation questions, a calculator is often not allowed. In other cases, these questions can be so strictly timed that you don’t even have enough time to reach a calculator. It’s best that you can prepare well, instead of relying on devices.

Calculation (No word problem)

Calculation (No word problem) questions require you to conduct basic mathematical operations such as addition, subtraction, division, and multiplication while also testing your performance on arithmetic terms and methods such as percentages, ratios, and fractions.

This type is presented in the form of plain calculation questions that are designed to only test your calculation abilities, not your reasoning process or your problem-solving process.

For example:

1. 36 + 57 = 87 + ?
2. 145 – 87 = ? – 98
3. 4.5 x 2.3 = ?
4. 17% of 900 = ?
5. 885 : 4 = ? 

Word problem 

Word problem questions still involve basic mathematical operations but within a word context. Other than simply delivering math calculations, you’ll have to take an extra step to extract the numbers and information you need for the actual computation.

Both of these question types often come in the form of multiple choices, and you’ll need to be extra careful of distracting answers – the ones that are either extremely similar to the correct answer or easily made out of common math mistakes.

For example: 

Estimation

Numerical estimation questions target evaluating your estimating ability, which is also a part of mental math skills. Estimation questions involve making quick and accurate estimates under the pressure of time without a calculator. This is critical for clerical and administrative positions, and also jobs in craft and technical fields.

One important thing to keep in mind when doing estimation is not to waste time calculating the exact answer. Depending on the instructions, you can decide how much you should round up each number before making estimations.

In most cases, the instruction tells you to look for the closest answer; therefore, your estimating calculation should be within a small margin of error.

The only way to reach a balance between accuracy and speed for these types of questions is through practice, although it might take some time. By practicing, you can figure out your compromising point between speed and accuracy.

This type of question often appears in the form of gamified assessments. Take a look at this example:

Source: JobFlare – Criteria Corp

Numerical sequence

Numerical sequence or numerical series questions demonstrate a sequence of four to seven numbers that are in an arithmetic relationship. Candidates are required to figure out a logical pattern behind the numbers, and use it to find the next number in the sequence.

In these numerical sequence questions, you are often allowed to use a calculator. This is because the main purpose of these questions is not to test your calculation abilities, it is to test your reasoning abilities in how you recognize the sequence pattern.

For some questions, you can easily work out the pattern but in harder ones, you’ll have to make a few guesses before getting the correct logic. In such cases, a calculator that can work with ratios and percentages will be of great help.

For example:

Source: Cubiks

Data interpretation

In data interpretation questions, candidates are provided with statistical data in tables, graphs, and charts, and asked to draw conclusions from such data. You should prepare to handle these questions when applying for jobs requiring numerical data analysis or decision-making such as consultants, accountants, business managers, data analysts, and IT developers.

Data presentation of these questions can fall into certain categories as below:

• Tables
• Bar charts
• Line charts
• Pie charts
• Caselet (data is provided in a paragraph)
• Mixed

Data interpretation questions are often delivered in two different levels of difficulty: Intermediate and Advanced.

• You only need to work on ONE table/chart/graph at the intermediate level. The question is straightforward and only requires one calculation to reach the final answer.
• At the advanced level, the question often involves at least two sources of information (table/chart/graph), and to work out the answer, you need to perform two or more calculations. Although the calculations aren’t necessarily complicated, you’ll find it confusing when locating the data you need. You’ll either encounter too many distracting details or combine many charts for the required data. 

To handle these data interpretation questions, here’s our five-step suggestion:

Step 1

Study the charts and see what kind of data they present. If there is more than one chart, make sure you figure out the relations among them.

Step 2

Go through the questions to understand what kind of data you need.

Step 3

Locate and extract the information you need from the corresponding table/graph/chart.

Step 4

Use the data to compute the answer.

Step 5

Make meaningful inferences from the numerical answer if the question requires you to do it.

For example

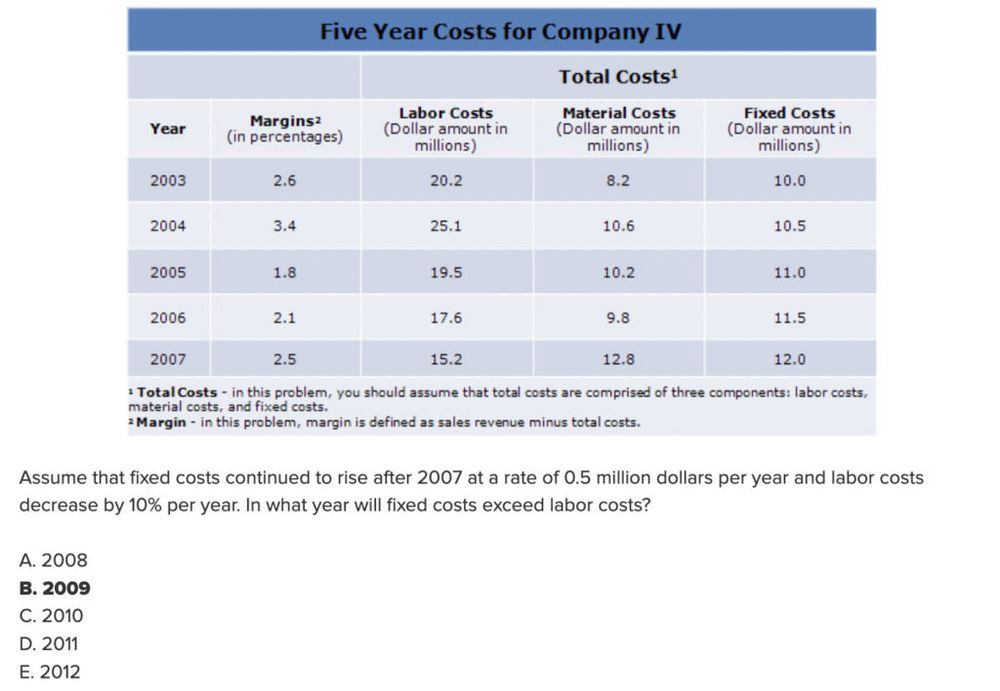
Answer: B

Explanation: In 2008, fixed costs will have risen to $12.5 million and after decreasing by 10%, labor costs will be $13.68 million. Labor costs are still higher, therefore, we would continue and examine this for the following year. In 2009, fixed costs will have risen to $13 million, and labor costs will have decreased to $12.31 million. Now fixed costs are higher. Hence, the correct answer is 2009.

KEY TAKEAWAY

80% of numerical tests are Word Problem and Data Interpretation questions. Our numerical reasoning package provides you with exactly what you need: 500+ questions with various difficulty levels plus an in-depth study guide and answers guides. All aim to help you to get the best results in the actual tests.

What do numerical reasoning tests measure?

Numerical reasoning tests, also known as numerical aptitude tests, are designed to measure the abilities of test-takers in solving basic math calculations, as well as analyzing, interpreting, and drawing conclusions from different forms of data sets.

Numerical reasoning tests measure calculation abilities

Numerical reasoning tests measure your calculation abilities through multiple types of questions in the tests. In the purest form, numerical reasoning tests assess calculation skills by grading how well you score on math questions that involve decimals, percentages, ratios, etc., and basic principles of arithmetic such as addition, subtraction, multiplication, and division.

In most cases, simple calculation questions are not to test your reasoning abilities or your problem-solving process since to perform well on such questions, you only need to make quick and accurate calculations. There’re some tips to help you with improving your calculation-solving speed which we’ll mention later in this article.

In other forms of questions other than plain numerical calculations such as data interpretation, calculation abilities are not the main evaluating criteria but rather a means of helping you to arrive at the final result.

Numerical reasoning tests assess data analyzing competence

Numerical reasoning tests assess your data analyzing competence in questions involving math problems in a word context or data presentations. You will be given either sufficient or abundant data that requires you to work on and figure out how to arrive at the final answer.

In other words, you’ll need to read and analyze data within a specific context and decide what information and calculation are required to answer the question.

Numerical reasoning tests evaluate data interpretation skill

Numerical reasoning tests also evaluate your data interpretation skill when asking you to draw specific conclusions from your previous calculations. These targeting questions are commonly seen in numerical reasoning tests in consulting and business fields.

Questions testing interpretation skills often use workplace-based materials appropriate to the role and level at which the candidate is applying, and therefore the result allows recruiters to see whether the candidate possesses requisite skills.

What skills to practice for numerical reasoning tests

Four fundamental math skills you should focus on practicing for the test include:

• Basic numerical operations
• Mental math
• Metric measurement
• Complex mathematical operations

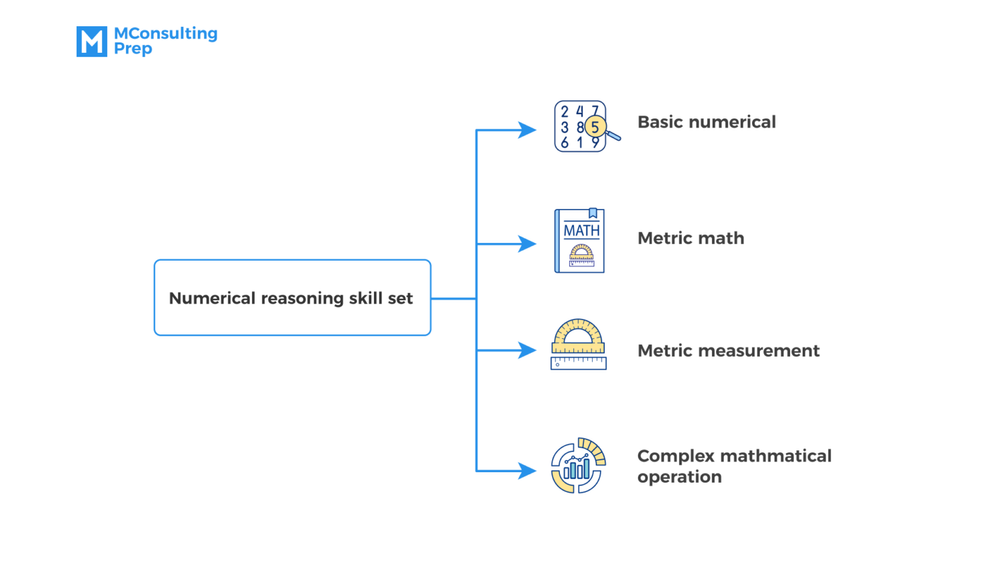
Numerical reasoning tests are not designed to test math skills, but rather to see how you process data and apply math skills in getting the answer. Nevertheless, you still need to practice these key math skills to help you speed up the problem-solving process.

Basic numerical operations

Addition, subtraction, multiplication, and division are four basic numerical operations you need to master before taking numerical reasoning tests.

As basic as these math operations are, they are fundamental in every numerical reasoning question. Excelling at doing these foundational operations helps you save time for more complicated questions, increase accuracy, and gain easy marks.

When doing math operations, you should keep in mind the sequence that needs to be followed to do calculations properly. Addition and subtraction are first-level mathematical operations, while multiplication and division are second-level mathematical operations. For that, it means:

• If it’s a math operation of the same level, we resolve it in the order from left to right;
• If it involves operations between different levels, we resolve it by the level order (Addition, subtraction first, and multiplication, division after).

Mental math

Mental math is a crucial factor that decides the speed and accuracy of your performance in tests like numerical reasoning, where calculators are mostly not allowed. Nevertheless, in almost every numerical reasoning test, it is by default that you’ll be dealing with huge numbers and values.

A standard numerical reasoning test often consists of 60 questions, and a test-taker is expected to handle approximately 200 math operations. About 80% of these operations can be completed in a matter of seconds, while the rest might require more time and effort. For that, mental math is necessary if you want to ensure accuracy within the time allowance.

To advance in mental math, you can practice it with several calculation tips. Below are a few tips that might be helpful for you.

Tip 1: Round up numbers

Making calculations with big numbers can sometimes be difficult, and rounding them up is an effective way to deal with such calculations. You should only round up numbers to the nearest unit (i.e 856 becomes 860, not 900), so it doesn’t take you much time to find the exact answer from the round-up result.

Example: 657 + 249 = ?

To solve this, we start by rounding up each of these numbers. So, 657 becomes 660, and 249 becomes 250.

Then we resolve the math problem with the new numbers, which is 660 + 250 = 910.

Now we see what’s been added up to the original numbers:

660 – 657 = 3

250 – 249 = 1

So to find the exact answer, we just need to deduct 4 from the sum, which is 910 – 4 = 906.

Tip 2: Take out the zeros

In calculations having many zeros, you do these calculations in plain numbers without the zeros and finish by adding back the number of zeros you take away.

Example: 5000 x 7600000 = ?

First, we calculate the multiplication in plain numbers, which is 5 x 76 = 380.

We see that there is a total of 8 zeros following the numbers, so we put those back to the above result of 380.

The final result of the calculation of 5000 x 7600000 will be 38 000 000 000.

Tip 3: Flipping percentages

The percentages can be switched in the multiplication of two-digit numbers. So if you can not find the answer to a certain percentage multiplication, you can try to switch them around.

Example: Calculate 67% of 10

We can calculate 10% of 67 which is the same as 67% of 10, while the calculation process can be much faster.

Tip 4: Moving decimals in multiplications, and divisions with 10% and 1%

For multiplications with 10% and 1%, you don’t need to calculate. All you have to do is to move the decimal one or two places to the left of the original number.

Example: Calculate 10% of 86

We solve this by moving the decimal one place to the left of the original, which is 8,6.

Example: Calculate 1% of 86

We solve this by moving the decimal two places to the left of the original, which is 0,86.

For divisions with 10% and 1%, you only need to add one or two zeros; or move the decimal one or two places to the right of the original number.

Example: 86 ÷ 10% = ?

We solve this by adding one zero to the right of the original, which is 860.

Example: 86 ÷ 1% = ?

We solve this by adding two zeros to the original’s right, 8600.

Example: 0,86 ÷ 1% = ?

We solve this by moving the decimal two places to the original’s right, 86.

Tip 5: Multiply two-digit numbers by 11

For numbers whose sum of the two digits is smaller than or equals 9, you just need to put the sum between these two digits.

Example: 45 x 11 = ?

We find the sum of the two digits, which is 4 + 5 = 9.

Then we put the sum between the two digits for the final answer, which is 495.

So, 45 x 11 = 495.

For numbers whose sum of the two digits is greater than 9, you’ll need an extra step. Here’re the steps:

You’ll find the sum of the two digits as usual.

You continue to calculate another sum of the number’s first digit and the sum’s first digit.

Now place the second digit of the first sum between the second sum and the second digit of the original number.

Example: 78 x 11 = ?

We find the sum of the two digits, which is 7 + 8 = 15.

Then we find the second sum, which is 7 + 1 = 8.

Then we place the second digit of the first sum (5) between the second sum (8) and the second digit of the original number (8), and we have the final answer which is 858.

So, 78 x 11 = 858.

Metric measurement

Below are the most popular measures of numeracy that you can come across in a numerical reasoning test:

• Time: Hour, minute, second, year, month, week, day
• Distance: mile, foot, km, m, cm, mm
• Velocity: km/h, mph, m/s
• Weight: kg, g
• Money: £ and pence; $ and cent
• Volume: liter, milliliter
• Degree: ℉, ℃

To handle these kinds of questions, you’ll need to invest your time in memorizing the value-exchange rules and practicing. Practicing is the key to achieving accuracy within the timeframe of the test.