How to Subtract Fractions With Different Denominators?

Subtracting fractions with different denominators does seem difficult, especially when working with big numbers. However, once you get to know the steps and tips, such calculations are not as complex as they seem. Below we will provide you with a four-step approach and several tips that help you solve fraction subtractions easily.

Learn more: Numerical Reasoning Tests Guide

Subtracting fractions in four steps

The four-step approach is a traditional method that is applicable to all cases, regardless of the fraction types you’ll be dealing with.

Before proceeding to the first step, it’s necessary to understand the structure of a fraction. A fraction has two parts which are the numerator and denominator separated by a dividing line. In a subtraction or an addition with fractions, we need to ensure that the denominators of two or more fractions in the calculations are the same before actually calculating.

Below are details of the four steps that will help you with fraction calculations. For you to get a better understanding of our four-step approach, we will work out the same example throughout the four steps.

Step 1: Figure out the least common denominator

The least common denominator is the lowest common multiple of two or more denominators in the fraction subtraction you’re working on.

To find the least common denominator, we find the smallest number that is divisible by both of the denominators. In this case, the least common denominator is

17 x 6 = 106.

Step 2: Figure out the equivalent fractions 

After finding the smallest common denominator, you need to figure out what the new fractions are when both of the fractions now have the new denominators.

Working the same example from step 1, we have the new denominator of both of the fractions is 106.

For the fraction of 13/6 to change its denominator into 106 while keeping the same value, we multiply both the numerator and denominator with 6. 

Step 3: Do the subtraction

Now with the new fractions, we just need to do the subtraction of the numerators for the result.

Step 4: Simplify the result if needed

For the final answer, you’ll need to simplify the fraction result if necessary. In the given example, 167106 can’t be simplified as the numerator and the denominator aren’t divisible by any whole number.

In other cases where numerators and denominators are divisible by a whole number, you have to simplify the fraction by dividing both of the numerator and denominator by that number. You continue such a process until the numerator and denominator aren’t divisible by any whole number anymore.

Tips on subtracting fractions with different denominators

Although you can use the four-step approach for all fraction subtractions, sometimes it’s not the most time-saving method to do fraction subtractions. Below we have a few tips to help you do fraction subtractions in a much faster manner.

Tip 1: Cross-multiplying before subtracting

This is the easiest way to do subtractions of fractions with different denominators. Here are the step details with an example.

Step1: We find the value of the fractions’ cross-multiplication, which is (2×7) and (1×5)

Step 2: We find the value of the subtraction between the above result, which is

(2×7) – (1×5) = 9. This number is the final answer’s numerator.

Step 3: Find the denominator of the final answer by multiplying the denominators of the two fractions in the subtraction, which is 5 x 7 = 35.

Tip 2: Detect the least common denominator in the subtraction

You don’t have to always multiply denominators to find the least common denominators. Sometimes the least common denominator can be one of the fractions’ denominators. You need to see if one of the fractions’ denominators is divisible by the other denominator.

Tip 3: Check if the fractions can be reduced to simpler forms

It’s much easier to do calculations with small numbers, therefore you should always check to see whether the given fractions are in their simplest forms. In case they are not, reduce them to their simplest forms before making any calculations.

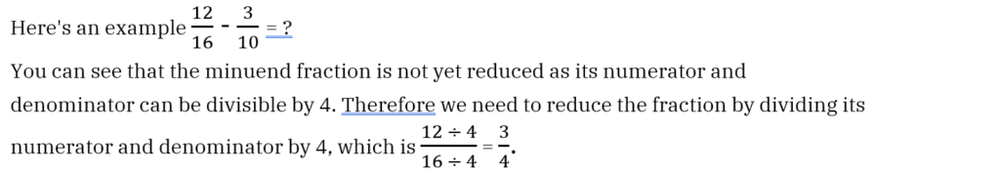
Now we can do the fraction subtraction using the tips or the four-step approach as usual.

In this case, we can see that the least common denominator is 20 and then we find the new fractions with the new denominators of 20.

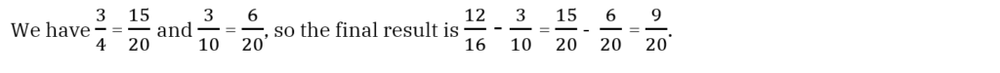
Practice examples

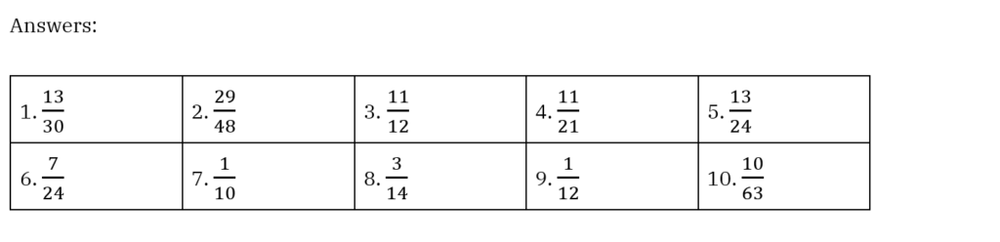
We have some more examples here for you to practice the four-step approach and the tips.

You can find more practice examples in MConsultingPrep's numerical reasoning test package! We even offer the free trial version to help you explore without any commitment!