Deductive reasoning is considered one type of logical thinking that involves the process of reaching a specific conclusion from a given general idea.
In this article, you will learn more about deductive reasoning, its applications, and examples in the workplace.
Table of Contents
What is deductive reasoning?
Deductive reasoning or deductive logic is a mental process of logically drawing valid inferences. In deductive reasoning, if the given facts, properties, or premises are true, and you apply the correct logic for the inferences or the conclusions, those inferences and conclusions must be true.
Deductive reasoning is also referred to as deductive logic or top-down reasoning.
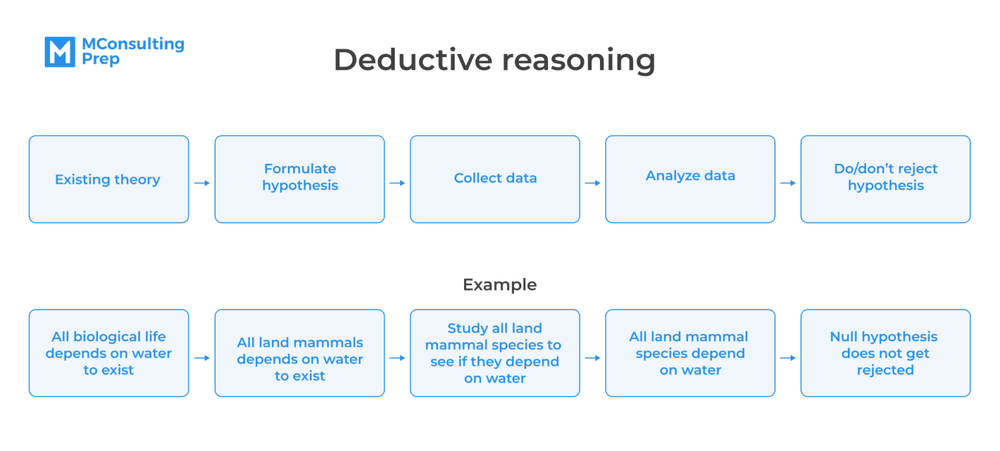
Deductive logic arguments
In deductive logic arguments, you are provided with one to several different premises (generally accepted ideas, facts, or rules which are statements that lay the groundwork for the conclusions) and you make conclusions (statements supported by premises) based on such premises.
Here’s an example for you.
Premise 1: All spiders have eight legs.
Premise 2: A tarantula is a spider.
Conclusion: Therefore, tarantulas have eight legs.
Deductive validity and Deductive soundness
A deductive argument must meet two requirements of validity and soundness.
In terms of validity, it is the way the given premises relate to each other and the inference or conclusion that is drawn from such premises. A “valid” deductive argument is a statement where the conclusion logically follows the premises; in other words, the truth of the premises guarantees the truth of its conclusion. It is IMPOSSIBLE for the conclusion to be true if the premises are false and vice versa.
Here is an example of a “valid” but untrue deductive argument.
Premise 1: All Greek men have beards.
Premise 2: Aristotle is a Greek man.
Conclusion: Aristotle has a beard.
This is a valid deductive argument yet not a true deductive argument since one of the given premises is not a true statement.
Due to the difficulty in identifying the logical relationship of an argument, and the potential deviation of logical relationship from a grammatical form in ordinary language, contemporary logicians typically adopt artificial languages that are similar to those used in mathematics to indicate those logical elements of such relationship. We often see certain symbols or words such as “all”, “not”, “or”, “and”, and so forth in the premises and conclusions of a deductive reasoning argument.
Using such artificially constructed language helps specify a set of rules that guides us toward determining the validity of a certain argument. Therefore, the study of which deductive argument relationship is valid or invalid is often referred to as “formal logic” or “symbolic logic”.
In terms of soundness, a “valid” deductive argument is also a sound argument when it has TRUE premises. You can still have a valid argument when the premises of your argument are false, as long as the conclusions logically follow the premises. But to have a sound argument, the premises of your argument are necessarily true.
Here is an example of a valid and sound deductive argument.
Premise 1: The solar system is in the Milky Way.
Premise 2: The Earth belongs to the solar system.
Conclusion: The Earth is in the Milky Way.
This is a valid and sound deductive argument since both of the given premises are true statements/facts.
Deductive reasoning tests in recruitment
Deductive reasoning is a required skill in many jobs, especially occupations in law enforcement and science fields. Therefore many employers have adopted deductive reasoning tests as one of the pre-interview tests to select the most appropriate candidate for each specific position.
Read more: Are Deductive Reasoning Tests Hard?
While there are a significant number of deductive reasoning test providers, it’s more likely that you encounter deductive reasoning tests of CEB SHL and Kenexa – the two most popular deductive reasoning test providers.
Different types of deductive reasoning
There are three common types of deductive reasoning, which are
- Syllogism
- Modus ponens
- Modus tollens

Syllogism
A syllogism is a logical argument that uses deductive reasoning to arrive at a conclusion based on two premises (or propositions) that are asserted or assumed to be true. The general form of a syllogism includes a major proposition, a minor proposition, and a conclusion.
In a syllogism, the major premise contains the major term which is the predicate of the conclusion; the minor premise contains the minor term which is the subject of the conclusion. The premises also have the middle term which is not included in the conclusion but once in each premise.
In a major premise, the major term can appear in either the subject position or the predicate position. The same thing applies to the minor term.
There are three main types of syllogisms as follows:
- Conditional syllogism: If A is true then B is true (If A then B).
- Categorical syllogism: If A is in C then B is in C.
- Disjunctive syllogism: If A is true, then B is false (A or B).
There are five rules a standard-form syllogism must follow to be valid. If a syllogism fails to meet any of these rules, it is then invalid. Below are the five rules that enforce the validity of a syllogism with a potential fallacy that indicates the syllogism’s invalidity:
- The middle term must be distributed at least once. The fallacy lies in the undistributed middle term;
- If a term is included in the conclusion, it must also be in its corresponding premise. The fallacy lies in either the undistributed minor term in the subject or the undistributed major term in the predicate;
- A syllogism cannot have two negative premises. The fallacy lies in the exclusive premises;
- A negative premise must have a negative conclusion and vice versa. The fallacy lies in either stating an affirmative conclusion based on a negative premise or stating a negative conclusion based on an affirmative premise;
- Two universal premises must have a universal conclusion. The fallacy lies in the particularity of the conclusion.
Modus ponens
Modus Ponens (also known as affirming the antecedent) is a type of deductive reasoning. In a Modus Ponens argument, the first premise is a two-clause conditional statement, the second premise is an affirmation indicating that the if clause is true, and the conclusion is an affirmation of the second clause.
For example:
Premise 1: If it rains on Monday, all flights to New York are canceled.
Premise 2: It’s Monday and it’s raining.
Conclusion: All flights to New York are canceled.
Modus tollens
Modus Tollens (also known as the law of contrapositive) is another type of deductive reasoning. A Modus Tollens argument is opposite to a Modus Ponens argument in which the second premise is a negative indication of the second clause of the conditional statement, and the conclusion is also a negative indication of the if clause.
For example:
Premise 1: If a person is born between 1945 and 1965, then they’re a baby boomer.
Premise 2: Alice is not a baby boomer.
Conclusion: Therefore, Alice was not born between 1945 and 1965.
Deductive reasoning vs. Inductive reasoning
Deductive reasoning is a top-down approach that you use when making inferences from general premises, or in other words, you go from general ideas to more specific statements.
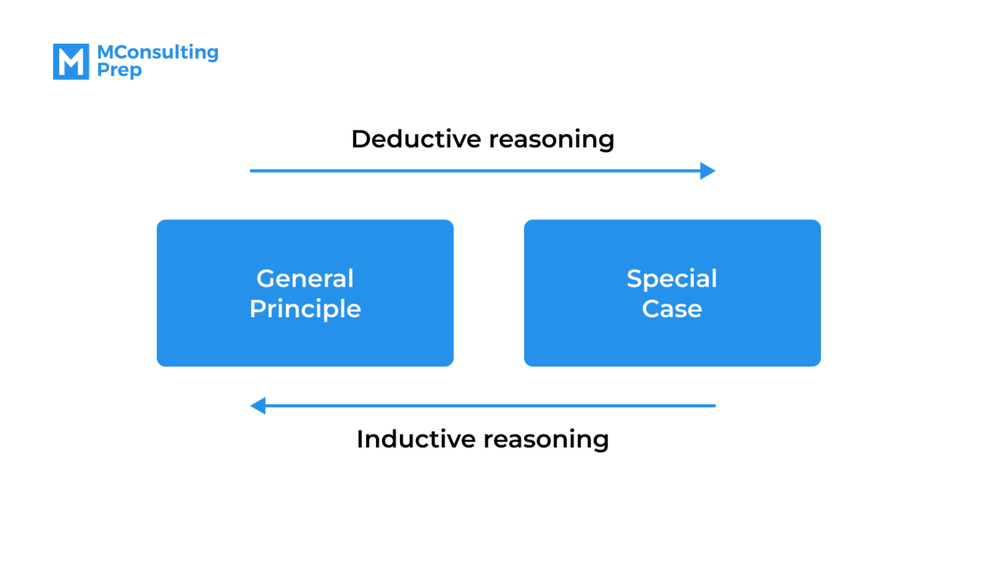
On the other hand, inductive reasoning is a bottom-up approach that you use when delivering a general idea from a specific statement. Inductive reasoning can not ensure an absolute certainty of the conclusion but instead reinforces that an inductive reasoning conclusion based on given premises is more likely than not to be true.
It is a stark difference from deductive reasoning that, while inductive reasoning cannot guarantee a certain conclusion the way deductive reasoning can, it can help deliver predictions about future events or as-yet unobserved phenomena.
If deductive reasoning is about your ability to make sound and valid judgments/conclusions based on general concrete data, inductive reasoning focuses on your capability to recognize meaningful patterns and connections based on scattering details.
Deductive reasoning vs. Abductive reasoning
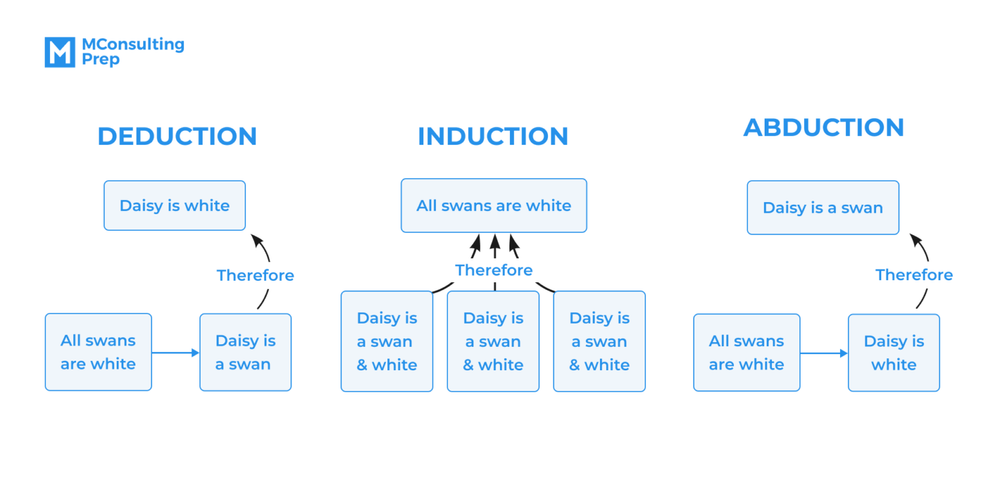
If deductive reasoning gives you evidence to confirm your hypothesis, abductive reasoning gives you evidence to generate a hypothesis. The stark difference between these two kinds of reasoning is that deductive reasoning gives you a general statement to base your hypothesis on and arrive at a conclusion for the hypothesis; abductive reasoning only gives you a certain case to arrive at a hypothesis that may or may not be valid.
Abductive reasoning arguments are all about arriving at a possible conclusion or explanation (hypothesis) for a certain case or set of information. Abductive reasoning is much like inductive reasoning in the way that it gives you information to generate a pattern, connection, or explanation for certain incidents. The only difference between these two kinds of reasoning is that deductive reasoning only gives you a small amount of information to GENERATE a hypothesis, while inductive reasoning gives you a considerate amount of information to TEST & PROVE a hypothesis.
Examples of deductive reasoning
Example 1:
It’s dangerous to drive on wet streets (premise 1). The streets are wet now (premise 2), so it would be dangerous to drive on these streets.
-> This is a valid and sound deductive argument since both of the premises are true statements.
Example 2:
All the time-counting instruments are watches (premise 1). Some time counting instruments are alarms (premise 2), so some alarms are watches.
-> This is a valid and sound deductive argument since both of the premises are true statements.
Example 3:
Sunflowers are plants (premise 1), and all plants perform photosynthesis (premise 2).
Therefore, sunflowers perform photosynthesis.
-> This is a valid and sound deductive argument since both of the premises are true statements.
Example 4:
All polar bears are white (premise 1).
Thomas is white (premise 2).
Therefore, Thomas is a bear.
-> This is a valid deductive argument yet not a sound deductive argument. This is because none of the premises are facts or true statements.
Example 5:
At least some Danish are Scandinavian (premise 1).
Every Scandinavian is a European (premise 2).
Some European is an American (premise 3).
Therefore, some Danish could be American.
-> This is a valid and sound deductive argument since all of the premises are true statements.
You can find more 200+ examples of deductive reasoning question through this link. Feeling unsure to spend your money? MConsultingPrep offers Free Trial for you to experience!
/filters:quality(75)//case_thumb/public/1699589977462_aptitude_tests_package_4_x.png)